A version of this post is also available as a YouTube video here.
In this post I want to look at the physics of a playground swing, and how we can pump it to get higher. There are actually two different methods of pumping a swing: a seated method and a standing method. In my post and video I focus on the seated method.
I used a model from Hirata et al (2023) in which the human body is approximated by three segments, and the chain of the swing is assumed to remain straight. I took the Euler-Lagrange equation from the paper, with minor fixes1, and ran it forward in time using a Runge-Kutta method. My source code is available here and includes the parameters I used.
This is the result, and despite being just a graph with a handful of lines, it does show impressive resemblance to a human pumping a swing:
The basic physics
The basic physics is not difficult to understand. Here I will refer to the chain, the seat and the person on the swing (swinger?) as “the swing system”. By leaning his or her body, the swinger can adjust the center of mass of the swing system, as represented by the red dot in each of the following diagrams:
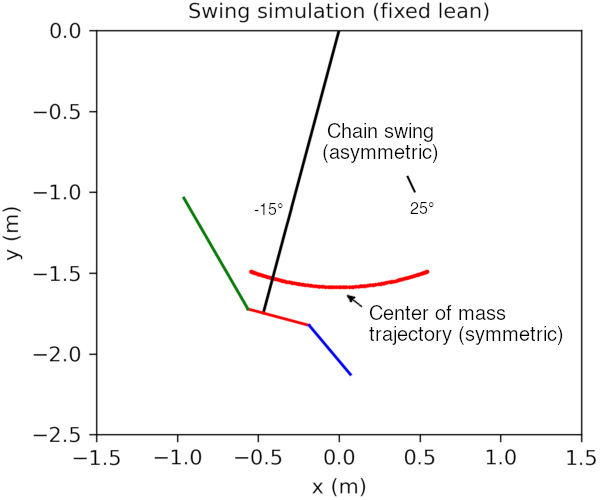
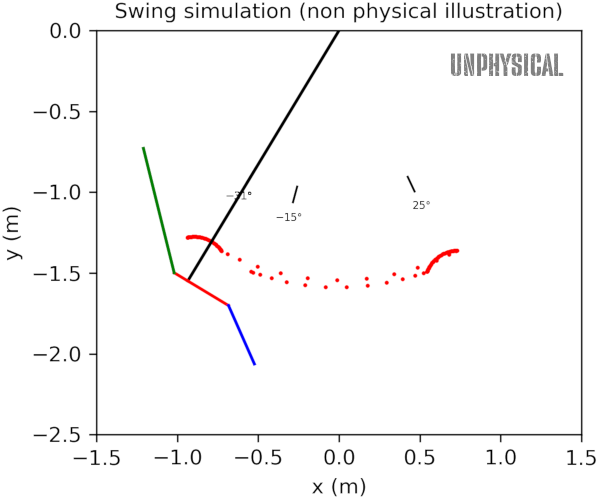
Consider what happens if the swinger adopts a constant lean while swinging. The center of mass of the swing system oscillates symmetrically like a normal pendulum, but the chain travels higher on one side:
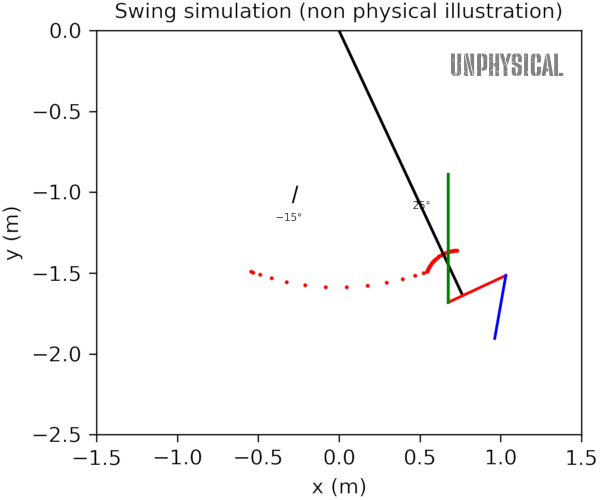
The swinger can use this to their advantage. Upon reaching the right side, which has a high chain position and low center-of-mass position, the swinger leans forward, pulling up their center of mass towards the chain:
Now the pendulum swings from a higher position, and we have added energy to the swing system. Upon reaching the left side, we are again in a situation of high chain position and low center-of-mass position, and we can lean back to perform the trick again:
You will notice that I have written “unphysical” across these graphs, because while they should provide the correct intuition about how we pump a swing, there are two issues we must address:
- It is not possible for the swinger to switch position instantaneously at each end, and
- We have ignored the reaction forces on the swing when the swinger changes position.
Actually these two issues are somewhat linked, because more rapid accelerations from the swinger result in higher forces. We also need to address how the swinger can pull up the swing system’s center of mass at all.
By the bootstraps
Anyone who has considered this problem before has probably wondered how the swinger can “pull themselves up by their own bootstraps” while inside the swing system. From Newton’s laws, we need an external force to change the center-of-mass velocity of a system. Neglecting aerodynamic drag, the external forces on the swing system are gravity and the forces at the pivot point.
If the swinger wants to raise the center-of-mass of the swing system, the only external force they can leverage is that at the pivot point. So we should take a digression into what happens at the pivot point.
On forces at the pivot point
It is often considered that the only force at the pivot point is tension in the direction of the chain/rod/rope. While this may be technically true for a flexible rope, I think it can be misleading to look at it this way.
First consider the case of a rigid rod:
If we push the rod to the right a little, there must be a reaction force at the pivot towards the left, otherwise the whole rod would start travelling to the right (as well as starting to rotate). It is clear that in this rigid case, the forces on the pivot point are definitely not constrained to being along the rod.
Now consider a flexible rope with a mass on the end:
If we push the mass to the right a little, we send a transverse wave up the rope. If the pivot is unconstrained horizontally, it will slide when the wave reaches it. Again a horizontal reaction force at the pivot point is required to keep the pivot point fixed. Now instantaneously the force from the rope will be in the direction of the rope, when the rope is considered with the wave superposed on it, but it is not necessarily in the direction towards the mass.
(In the real world, there is no perfectly rigid object, and these two cases are not really that distinct: in all cases transverse forces applied to the bottom of the chain are transmitted as transverse waves to the pivot. The velocity of the waves depends on the elasticity of the chain medium, and we can ignore the wavelike behaviour if the medium is very stiff.)
Returning to the problem
Let us now return to the previous statement: “if the swinger wants to raise the center-of-mass of the swing system, the only external force they can leverage is that at the pivot point”.
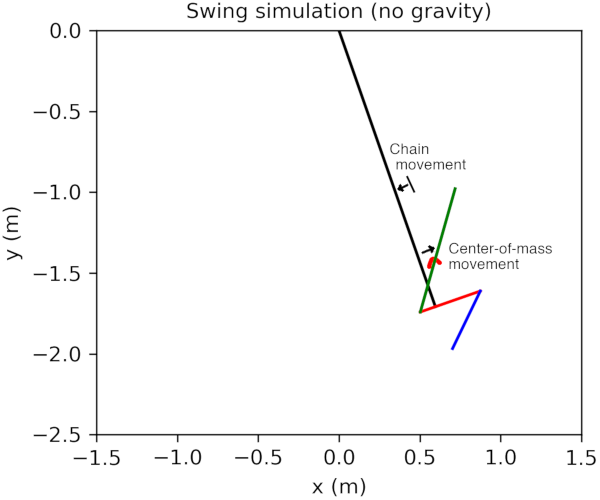
Originally we might have assumed that it is only possible to shift the center of mass in the direction towards the pivot, but given the discussion in the previous section it turns out that this is not true. Shifting the swinger’s center of mass outwards in the tangential direction results in an inward shift in the swing chain, as expected, but the cancellation is not complete and the center of mass does actually move outwards:
The dynamics of lean adjustment
Still, the swinger cannot change lean angle instantaneously at the two ends, and the swing continues to move during the adjustment. We can consider two different methods:
- A “jerky” method, in which the swinger changes their lean angle rapidly at each end of the swing. This maximises the theoretical gain from leaning, but the rapid acceleration also results in greater reaction forces on the swing, which tend to oppose the gain.
- A “smooth” method, in which the swinger moves as smoothly as possible (sinusoidally) to minimise accelerations and hence reaction forces.
In both cases the phase of the movement can be tuned for best results2. Simulation of the two approaches near their optimal phase angles shows that, for practical purposes, they perform similarly:
It is not clear to me whether there could theoretically be another movement schedule that is more efficient. But if there was, I would expect that human swingers would have found it.
On parametric resonance vs driven oscillation
Many authors dwell on the question of whether swing pumping is an example of parametric resonance or driven oscillation. It should be clear from Figures 1 and 2 that the primary motion being executed here is tangential movement of the center of mass. While there is some radial motion evident in Figure 2, it is brief and not resonant with the swing motion. Therefore we can say with some confidence that this is a case of driven oscillation, the driving force being the reaction force at the pivot that results from the swinger’s movements.
The curious case of the legs
If you examine Figure 1 again, you will notice that the motion of the lower legs is actually in the opposite direction to the desired center-of-mass shift. However this does not significantly affect the center-of-mass motion, since the mass of our lower legs is small compared to our upper body3.
Why swing our legs then? I think there are two reasons:
- Synchronized motion of the legs supplies opposing accelerations, reducing the reaction forces on the swing. Despite decreasing the center-of-mass shift slightly, it seems that overall there is a net benefit: there is a slight increase in gain per cycle, at least for the parameters studied here (the comparison is shown at 0:34 in the accompanying YouTube video).
- Swinging the legs may help with balance, although this effect may not be significant given the low mass of the legs as mentioned; holding on to the swing is still required when leaning.
On non-rigid chains
The same analysis can also be used as a first order approximation for swings with non-rigid chains, such as multi-link chains or ropes. Since the chains of playground swings are invariably light compared to the swinger, they tend to remain relatively straight under tension, and do not deviate greatly from rigid rods. In this case the geometry of the system is the same and therefore the mechanics is the same (this can be seen by, for instance, considering the system under Lagrangian or Hamiltonian mechanics).
A complication is the point at which the swinger holds the chain:
There are two basic reasons that the swinger will exert force through their arms, resulting in the chain bending. Firstly, some degree of force here is required to maintain balance when leaning. Secondly, some people use their arm muscles to assist in rotation of the upper body during the swing. However, the latter is not strictly necessary, as the rotation of the upper body can be achieved by the use of abdominal muscles instead.
A full analysis of the case of a non-rigid chain is complex and might be a good topic for an academic thesis. However to first order, we can see that when the chain bends, it works against the center of mass movement that we are trying to achieve:
For this reason I would humbly suggest that, contrary to the argument presented in a popular Sixty Symbols video, chain bending is actually counterproductive and should be limited to the minimum required for balance. Another recent paper by Murphy and Glendenning (2023) also contains a throwaway comment that appears to support this view (“of course, factors such as bend in the ropes […] will reduce the efficiency of the swing”). I am happy to be proved wrong on this point however.
Postscript: can you go “around the world”?
No discussion about swings would be complete without addressing the question that everyone always wants to ask: is it possible to go all the way around if you keep pumping? Let me summarize in the following table:
| Seated method | Standing method | |
| Swing with flexible chains/rope | No4 | Not recommended5 |
| Swing with rigid rods | Uncertain6 | Yes7 |
- In equation (2) -NLg sin θ should be -Ng sin θ, in equation (3) I think 8π should be 4, in equations (4) and (5) I think +αn should be -αn to match the semantics in the text. ↩︎
- For the smooth method, the maximum backwards lean should occur slightly before the bottom of the forward swing, with the exact timing varying slightly depending on swing amplitude. This is discussed in detail in the Hirata et al paper. ↩︎
- In the model, the lower legs are 6.4kg out of 50kg, while the upper body is 31.3kg out of 50kg; these numbers were derived by Hirata et al from prior published anatomical data. ↩︎
- It should be clear from the simulations here that each pumping cycle only gains a handful of degrees, and so it is not possible to pass through the upside-down region where chain tension is lost. ↩︎
- Standing pumping has less theoretical limits on gain per cycle, and Murphy and Glendenning (2023) suggest that it may be possible to turn over the swing with one explosive pump if the swing is small enough compared to the swinger. However I am dubious that this can be achieved in practice, and failure is not going to be pretty. ↩︎
- In the model here due to Hirata et al, it is possible to turn over the rigid swing if the drag term is removed, but with drag (representing both aerodynamic drag and friction at the pivot) the limit of pumping is around 160 degrees. Since the drag term is only an empirical model fitted to a given swing, it leaves open the possibility that it might be possible with a well-oiled swing at high altitude. In any case, failure on a rigid swing is less of a problem than failure on a flexible swing. ↩︎
- Exhibit 1, exhibit 2. ↩︎

 BETA
BETA