Magnetic field of a ferrite core solenoid

Consider a solenoid made of wire wrapped around a rod made of iron, ferrite, or other ferromagnetic material:

It is well known that the magnetic field will be significantly stronger inside such a solenoid, compared to an air core solenoid. The ferromagnetic core becomes temporarily magnetized and reinforces the magnetic field. But what I’m more interested in is: what is the effect of the ferromagnetic core on the field outside the solenoid, some arbitrary distance away? This question is interesting when using such a coil as part of a magnetically-coupled data or power transfer system, or when considering the electromagnetic interference produced by such a solenoid.

Some sources seem to suggest that the field will be confined more closely when a ferromagnetic core is used, as is the case for ferrite-core transformers. Other sources seem to suggest the opposite, namely that the ferromagnetic core increases the range of the field. Meanwhile a naive application of the Biot-Savart law would suggest that the field outside the solenoid does not change. Which of these is true?

Simulation

To answer this question, I ran a simple simulation with and without an iron core in the excellent FEMM field solver. Here is a picture of the results:

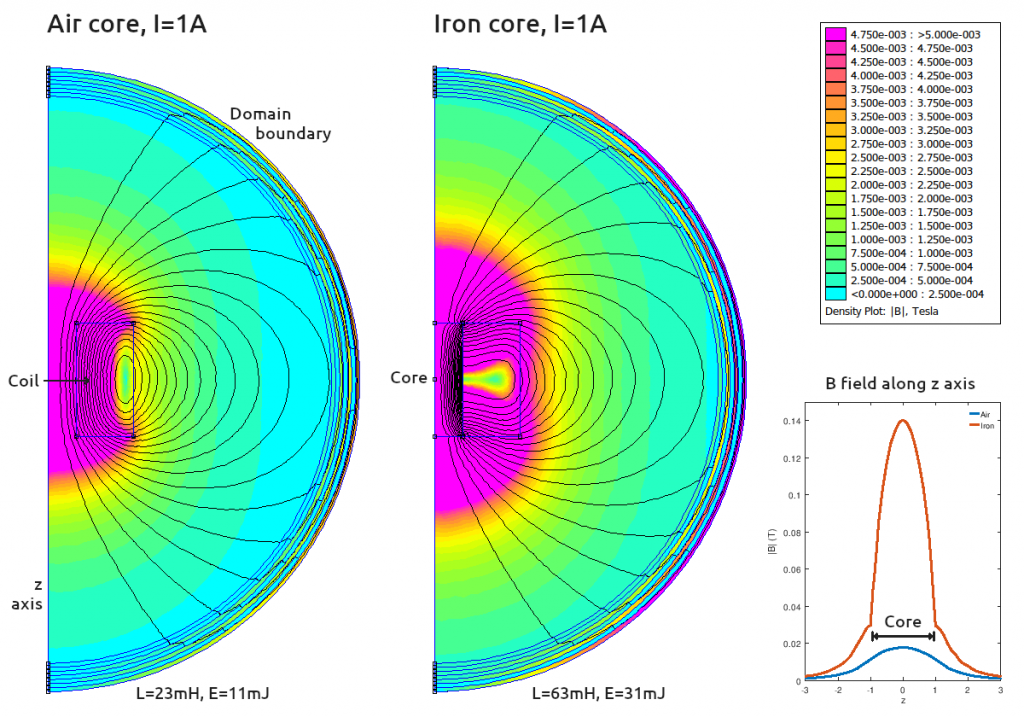
This is an axisymmetric simulation around the z axis. To picture the results in 3D, mentally revolve the half-circle about the z axis at the left. The outer sphere can be ignored, it is just the boundary of the simulation volume.

The conclusion from the simulation is that — at least for a fixed current — the magnetic field is higher outside the solenoid (at any given distance) when an iron core is added.

But surely as we learnt in physics classes, we should be able to calculate the external magnetic field by summing up all the current elements of the solenoid, per the Biot-Savart law? Why does adding an iron core make a difference?

I believe the explanation is that there are “bound currents” at the boundaries of the iron core which also need to be included in any such piecewise calculation of the magnetic field. This stackexchange answer has some good diagrams that help to explain how these bound currents come about.

Constant energy comparison

Now it should be noted that the above simulation has assumed a constant current of 1A in both cases. When the iron core is added, the inductance of the solenoid increases and we had to pump more energy into the solenoid to produce this 1A steady state — so perhaps it’s not surprising that the field is stronger outside the solenoid. To make a more “fair” comparison, I reduced the current through the iron core solenoid to produce the same total energy storage:

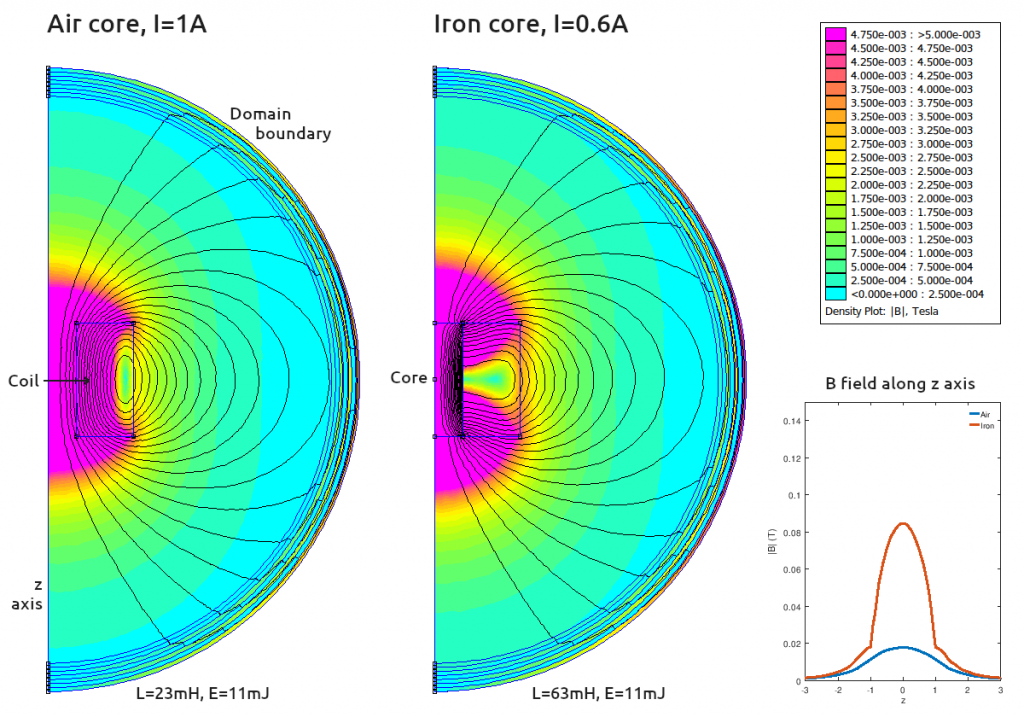
Notice that, at least for this geometry, the external magnetic field is still higher at any given distance.

“Return path”

So why do people consider iron/ferrite cores to confine fields more tightly? Well, the issue with the above solenoid design (or perhaps feature if you are trying to increase range) is that the return path of the magnetic field lines is through air and not through iron. We have boosted the magnetic field within the iron, but we’ve ended up with most of the field energy in the air.

If we were to put the iron all the way around the solenoid, which is closer to the usual design of transformers, the result does indeed confine the fields tightly (N.B. I have used the same colour mapping here so that it can be directly compared):

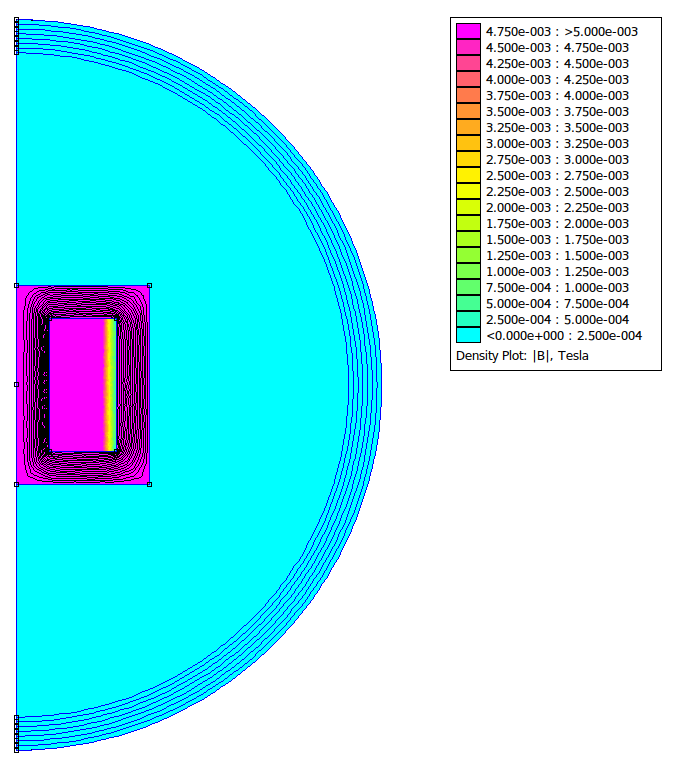
I hope that this post helps to clear up some confusion and might be of help the next time someone is searching for information about the external magnetic fields of ferrite core solenoids (like I was earlier today)! If you think I have got anything wrong, please let me know.