Directly downwind faster than the wind

Posted on May 31, 2024 by Matthew

A short version of this post is also available as a YouTube video here.

Is it possible to build a wind-powered vehicle that can continuously travel faster than the wind, in the same direction as the wind?

Like the airplane-on-treadmill problem and the Feynman sprinkler problem, this question has spawned endless Internet arguments. In 2010, Rick Cavallaro and team demonstrated a vehicle called Blackbird that officially reached a speed of 2.7 times the wind speed. But this just spawned more arguments. Indeed the design, in which the wheels are geared to a propeller, has all of the hallmarks of a perpetual motion machine, so it is understandable that some are skeptical. Here I want to present a thought experiment that might help to clarify some of the physics by reference to something more familiar: an airplane.

Preliminaries: Thrust

We start by considering a normal propeller-driven airplane. The propeller produces thrust, while aerodynamic drag retards the plane. When cruising at constant velocity, the thrust force T and drag force D are balanced.

Using an idealized physical model from momentum theory, we can derive a relationship between the power provided to the propeller and the thrust produced. The resulting simple equation can be found elsewhere, but I will derive it from first principles to expose the underlying assumptions.

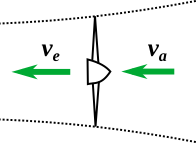
In the reference plane of the airplane, consider a streamtube of air that is accelerated by the propeller, from the ambient stream velocity va (= the plane’s airspeed) to some egress velocity ve. When following a given streamtube (bundle of streamlines), the streamtube must be narrower at the egress to produce the same mass flow:

Of course a real propeller is not as simple as this model: the spinning blades also accelerate some of the air in other directions, turbulent flows dissipate away some energy, and egress velocities are not perfectly uniform. But fundamental considerations of momentum and energy conservation must still bound the theoretical performance of the propeller. We will shortly add an efficiency factor to account for real propeller performance.

Considering momentum conservation: the propeller changes the momentum of air flowing through it, and thrust is the reaction force (where force = rate of change of momentum). Following standard physics conventions, I use a dot above a quantity to indicate a time derivative, i.e. rate of change with respect to time.

(1)   \begin{align*} T = \dot{p} = \dot{m}(v_e-v_a) \end{align*}

Considering energy conservation: the propeller must do work on the air stream to change its kinetic energy. The time derivative of this work is the power flowing from the propeller to the air.

(2)   \begin{align*} P = \dot{E} &= \frac{1}{2}\dot{m}(v_e^2 - v_a^2) \\ &= \frac{1}{2}\dot{m}(v_e - v_a)(v_e + v_a) \\ &= T v_a' \textrm{ where } v_a' = \frac{v_0+v_a}{2} = v_a+\frac{\Delta v}{2} \end{align*}

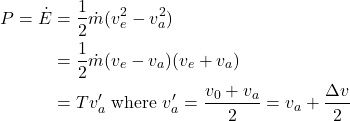
Reversing this equation produces thrust expressed in terms of the power flowing to the air. Then, we express thrust in terms of the input power Pin being provided to the propeller by the plane, by introducing an efficiency factor η:

(3)   \begin{align*} T = \frac{P}{v_a'} = \frac{\eta P_{in}}{v_a'} \end{align*}

η may depend on airspeed, but the important thing is that η ≤ 1 always. For any real propeller, η is strictly < 1: only some of the input power will result in thrust, while some will be lost elsewhere.

Independence of thrust from ground speed

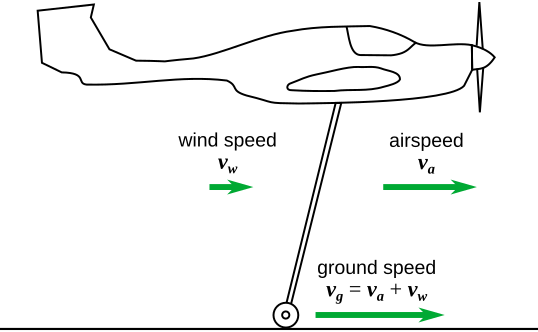
It is perhaps obvious, but it is worth stating explicitly: propeller thrust and resulting airplane velocity is purely with respect to the surrounding air, not with respect to the ground. If our hypothetical airplane is capable of an airspeed of 100 knots at a given engine power setting, and there is a 30 knot tailwind, the effective speed across the ground will be 130 knots.

Thought experiment, step 1

Now, we drop a long trundle wheel from our airplane to the ground and lock it into place. Conveniently, the ground is very flat everywhere in our Gedankenwelt, so the wheel can continue to roll unimpeded beneath the airplane. We can also ignore engineering problems associated with building such a long shaft; the airplane will fly as low as practically necessary.

Assume that the trundle wheel has negligible rolling resistance, and negligible wheel rotational inertia during acceleration. Then adding the trundle wheel has minimal effect on the flight of the airplane; it is simply rolling along under the airplane’s flight path.

(Note that I am defining ‘negligible’ such that this criterion is satisfied. If the effect on the flight of the airplane is not minimal, we can solve this by revisiting the engineering of the trundle wheel — higher pressure tyres, better wheel bearings, lighter materials, etc. — or perhaps using a more powerful airplane.)

Thought experiment, step 2

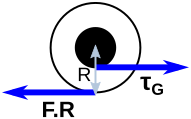
Next, we add a generator to the wheel axle. As an inevitable consequence of extracting power from the wheel’s rotation, the generator will produce a torque (τG) that will act to slow down the wheel. To prevent the tyre slipping, friction with the ground must counteract the generator torque. The torques on the wheel are shown in the following diagram (R is the radius of the wheel):

Note that if the airplane is accelerating or decelerating, the two torques here are not quite equal. A small part of the friction force is required to produce angular acceleration of the wheel, such that the circumferential velocity v=ωR always matches the linear velocity of the airplane and there is no tyre slip. But in step 1 we have engineered the problem such that that the wheel rotational inertia, and hence wheel-accelerating friction force F.R=Iα, is negligible. So, assuming that the magnitude of the airplane accelerations is not significantly different, we can ignore this Iα in step 2 as well.

(4)   \begin{align*} \tau_G - FR &= I\alpha \\ &\approx 0 \\ \Rightarrow \tau_G &\approx FR \end{align*}

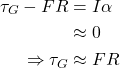
Assuming 100% generator efficiency, the power is then as follows (we can always insert a generator efficiency factor, but it does not affect the subsequent argument):

(5)   \begin{align*} P_{in} &= \tau_G \omega \\ &= (FR) \left(\frac{v_g}{R}\right) \\ &= F v_g \end{align*}

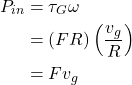
We can rearrange for the friction force F in terms of Pin:

(6)   \begin{align*} F = \frac{P_{in}}{v_g} \end{align*}

This friction force is an external force on the airplane system, and is adding an additional drag on the airplane alongside the aerodynamic drag. This is expected since power is being extracted by the generator. (Meanwhile the generator torque is an internal torque that does not appear in the subsequent free body diagram; we considered it here only as part of the derivation.)

Bringing it together

Now the question is, if we use power from the trundle wheel to drive the propeller, can we make the plane accelerate? Bizarrely, if the parameters are right, the answer is yes.

The reason that this works is that the power generated by the trundle wheel, for a given drag force, depends on the ground speed. But the thrust depends on air speed and not ground speed. So if there is enough difference between ground speed and air speed, we can have excess thrust. This is not a perpetual motion machine; the difference between ground speed and air speed is representative of the available wind energy.

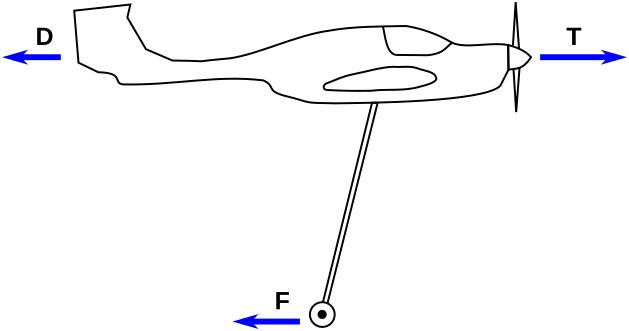
Let’s do the maths. Here is the final free body diagram:

The net horizontal force is the thrust minus the two sources of drag, and using the previously-derived expressions for T and F, this can be positive when the following holds:

(7)   \begin{align*} T - F - D &> 0 \\ \frac{\eta P_{in}}{v_a'} - \frac{P_{in}}{v_g} - D &> 0 \end{align*}

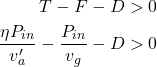
Focusing now on a faster-than-wind vehicle rather than a conventional airplane, the aerodynamic drag term D can be engineered to be small for two reasons:

  1. the operating speed is generally much lower than an airplane (and in air, drag is proportional to the square of velocity), and
  2. the airframe does not need to carry any significant payload, it can be no more than a propeller and associated linkages (in the case of Blackbird, the ground part of the vehicle does carry a driver, but it is very low to the ground and has reduced drag due to ground effect).

Then:

(8)   \begin{align*} \frac{\eta P_{in}}{v_a'} - \frac{P_{in}}{v_g} &> 0 \textrm{ as } D \rightarrow 0 \\ \eta &> \frac{v_a'}{v_g} \end{align*}

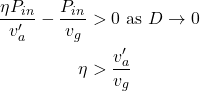
That is, to a first order approximation, the thrust is positive when the efficiency η of the power transfer from wheel to airstream exceeds the ratio between effective airspeed and ground speed. (Strictly speaking we have derived this taking η as propeller efficiency only, but we can also lump other efficiency factors into η.)

This is all consistent with sources that describe the mechanism as a sort of lever, but it can be difficult to intuitively visualize the lever.

Substituting for va‘ from equation (2) and va = vg – vw, we obtain the following equation that is even more immediately informative:

(9)   \begin{align*} v_g < \frac{v_w - \frac{1}{2}\Delta v}{1 - \eta} \end{align*}

Notice the following in particular:

  1. If there is no wind (vw=0), then there is no ground speed at which excess thrust is possible. There is no free lunch here, the energy must be coming from the wind somehow.
  2. The denominator approaches zero as the efficiency η approaches 1. Theoretically then, extremely efficient vehicles could operate at any multiple of the wind speed.
  3. To achieve 3x wind speed as in Blackbird, the power transfer efficiency from ground to air must be at least 67%. However in practice it will need to be rather higher to account for the Δv in the numerator of the above equation, for drag, and for other practicalities not included in this ideal analysis.

Note that this analysis is not intended to be completely sound for velocities less than wind speed. In this case, the airflow through the propeller could be in the opposite direction to the one analyzed when deriving T. But I think it is not in any doubt that a wind powered vehicle can travel at less than the speed of the wind. The Blackbird team has said themselves that in this sub-wind-speed regime, their vehicle accelerates simply due to wind drag.

Some final observations on (Galilean) relativity

While forces are the same in any inertial reference frame, energies are not. I would make the following observations:

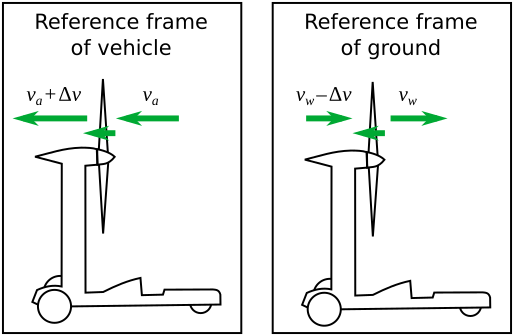
  1. In the reference frame of the vehicle, wind energy is flowing from the ground to drive the propeller, as demonstrated by the above thought experiment with the generator. It might seem odd to harvest wind energy from the ground, but remember that all velocities are relative, and the wind speed is meaningless except in relation to the ground. Think of the air and the ground as two large momentum reservoirs; it is the difference in the velocity of the two masses that is allowing energy to be extracted.
  2. In the reference frame of the ground, the propeller is slowing down the wind behind it (see below figure), and this is where the excess energy for acceleration must ultimately come from. In this sense the propeller is extracting energy from the wind. But I would not call this a wind turbine. A wind turbine is designed to capture energy from the wind as it passes through the turbine, by producing rotational motion of the shaft. In this case, the wind is not directly rotating the shaft, or observers in the two reference frames would disagree on the electric current flowing from generator to propeller (in our thought experiment version). Rather, I would suggest that the wind is helping to push the propeller and vehicle forward, such that the generator-propeller system can be less than 100% efficient and yet produce excess thrust.

Unfortunately, computing exactly how the wind interacts with the propeller is complex in the reference frame of the ground: a moving propeller is advancing through a moving medium. The human brain desperately wants to eliminate one of the relative velocities by imagining the problem in the reference frame of the vehicle or propeller blade or wind… but then we are no longer performing the analysis in the ground reference frame, and we must be careful about our conclusions when it comes to frame-dependent quantities like energy. For example, in a reference frame where the propeller is stationary, the air does no work on it, but this is not the case in the ground frame.

In the vehicle reference frame, the propeller is easier to analyze, but now the net energy flow is definitely into the propeller and it becomes more difficult to understand where this energy is coming from. This is especially true when travelling at wind speed and there is no apparent wind in the vehicle’s frame. However, in this reference frame the ground is moving. We simply must accept that the ground can be a source of wind energy, which makes sense when you consider the relativity of velocity.

This entry was posted in Physics. Bookmark the permalink.

Leave a Reply

Your email address will not be published. Required fields are marked *