-1/12 and the area under the sum function

You might have previously seen the assertion that:

$\begin{align*} 1 + 2 + 3 + ... = -\tfrac{1}{12} \end{align*}$

This is, of course, intuitively absurd. It is also properly absurd under standard rules of mathematics, so the use of an equals sign is reckless. The value -1/12 is obtained from either Ramanujan summation, or analytical extension of the Riemann zeta function and the subsequent assumption that ζ(-1) represents the sum 1 + 2 + 3 + ….

I shall not dwell too much on this topic as it is already well discussed elsewhere; for a gentle introduction I would recommend Mathologer’s video, or for a more technical but brilliantly accessible piece I would suggest Terence Tao’s blog post.

What I do want to dwell on is a curious fact pointed out by Mathologer at the very end of his video. It is well known that 1 + 2 + 3 + … + n can be evaluated via $\tfrac{n(n+1)}{2}$ or equivalently $\tfrac{1}{2}n^2 + \tfrac{1}{2}n$ , I will denote this function S₁(n). Consider the plot of the function S₁(n):

The yellow area is 1/12, in other words the integral over the interval [-1,0] is -1/12, the magic value referred to above. Co-incidence?

What if I told you that a similar property holds for other partial sums 1^p + 2^p + 3^p + … + n^p. For each value of p, we can obtain a polynomial S_p(n) that provides the correct sum, via Faulhaber’s formula. Integrating each of these polynomials over the interval [-1,0], the result matches the Riemann zeta function at –p, and also the value that would be obtained from Ramanujan summation of the corresponding sequence:

$\begin{alignat*}{5} \int_{-1}^{0} S_1(x) \mathop{dx} &= \zeta(-1) &&= -\tfrac{1}{12} \\ \int_{-1}^{0} S_2(x) \mathop{dx} &= \zeta(-2) &&= 0 \\ \int_{-1}^{0} S_3(x) \mathop{dx} &= \zeta(-3) &&= \tfrac{1}{120} \\ \int_{-1}^{0} S_4(x) \mathop{dx} &= \zeta(-4) &&= 0 \\ \int_{-1}^{0} S_5(x) \mathop{dx} &= \zeta(-5) &&= -\tfrac{1}{252} \\ ... \end{alignat*}$

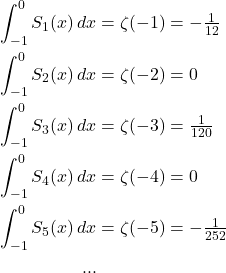
Integrating these sum functions from -1 to 0 seems like a very strange thing to do though. The original sum expression 1^p + 2^p + 3^p + … + n^p (i.e. $\sum_{k=1}^{n} k^p$ ) is only sensible for positive integer values of n. So we have already made a leap, analogous to analytical extension, by replacing it with a continuous polynomial over real numbers (that happens to match at the positive integers). And now we integrate this polynomial over negative numbers? What sorcery is this!

The meaning becomes clearer if we replace the -1 to 0 interval with a more general interval N-1 to N. We find that:

$\begin{align*} \int_{N-1}^{N} S_1(x) \mathop{dx} &= \tfrac{1}{2} N^2 - \tfrac{1}{12} \\ \int_{N-1}^{N} S_2(x) \mathop{dx} &= \tfrac{1}{3} N^3 \\ \int_{N-1}^{N} S_3(x) \mathop{dx} &= \tfrac{1}{4} N^4 + \tfrac{1}{120} \\ \int_{N-1}^{N} S_4(x) \mathop{dx} &= \tfrac{1}{5} N^5 \\ \int_{N-1}^{N} S_5(x) \mathop{dx} &= \tfrac{1}{6} N^6 - \tfrac{1}{252} \\ ... \end{align*}$

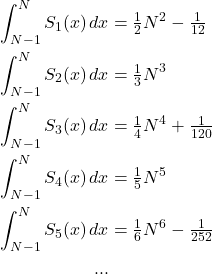
For the case of S₁(x), this is quite geometrically intuitive. Consider the following diagram of an arbitrary part of the curve:

The orange area (trapezoidal approximation) is $\tfrac{1}{2}N^2$ . The area of the parabolic sector is 1/12¹. Therefore the area under the curve is $\tfrac{1}{2}N^2-\tfrac{1}{12}$ . It should be clear from this construction that the -1/12 comes from the curvature of the function.

While the geometric construction is more complex for S_p(x) with p>1, it continues to be true that the constant comes from the curvature²; we can use the Euler-Maclaurin formula in this general case and the constant comes from a sum of derivative terms.

Now let us connect this back to Ramanujan summation.

Ramanujan’s approach to divergent sums is to first expand the sum using the Euler-Maclaurin formula:

$\begin{align*} \sum_{i=1}^{n} f(i) &= \int_{0}^{n} f(x) \mathop{dx} + \frac{f(n) - f(0)}{2}\\&\qquad + \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} \left(f^{(2k-1)}(n) - f^{(2k-1)}(0)\right) \end{align*}$

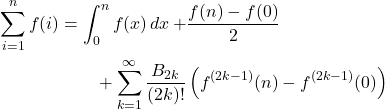
Now he splits out the constant terms that are not dependent on n (these arise from the function value and derivatives at the lower limit, in this case evaluated at 0). This he calls the sum, that is:

$\begin{equation*} C = -\frac{f(0)}{2} - \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} f^{(2k-1)}(0) \end{equation*}$

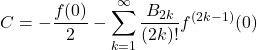
Consider now one of our functions f(x) = x^p, with S(x) being the corresponding sum function obtained via Faulhaber’s formula. Formally, S(x) can be defined by S(x)=S(x-1)+f(x) and S(0)=0. Applying the Euler-Maclaurin formula to S(x), with the integral rearranged to the left hand side:

$\begin{align*} \int_{-1}^{0} S(x) \mathop{dx} &= \sum_{i=0}^{0} S(i) - \frac{S(0) - S(-1)}{2}\\&\qquad - \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} \left(S^{(2k-1)}(0) - S^{(2k-1)}(-1)\right) \\[10pt] &= S(0) - \frac{f(0)}{2} - \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} f^{(2k-1)}(0) \\ & \qquad\text{since}\; S(x)-S(x-1)=f(x) \;\text{by definition of $S$} \\ & \qquad\;\text{and}\; S^{(k)}(x)-S^{(k)}(x-1)=\frac{d^k}{dx^k}\left(S(x)-S(x-1)\right)\\ & \qquad\qquad\quad\text{by linearity of differentiation} \\[10pt] &= - \frac{f(0)}{2} - \sum_{k=1}^{\infty} \frac{B_{2k}}{(2k)!} f^{(2k-1)}(0) \end{align*}$

We see that this is equivalent to the result from Ramanujan summation.

The slightly more rigorous procedure used by Terence Tao in his blog post also produces the same result given the assumption that “f vanishes to second order at N”. This leaves only the Euler-Maclaurin terms that relate to the lower limit, plus the integral term. Now it is clear that the original function, e.g. f(x)=x, does not vanish to second order anywhere. In fact it has a first derivative of 1 everywhere, in which case the sum is always $\tfrac{1}{2}N^2+\tfrac{1}{2}N$ as expected and no -1/12 appears! However, if we apply a cutoff function to tame the function at infinity, then regardless of the cutoff function, we “reveal” the -1/12 from the behaviour of the function at the lower limit.

Strangely these unexpected summation constants appear in some areas of physics, for example in calculations of the Casimir effect. I do not know whether this is related to the fact that no physical quantity can be unbounded — the universe always has some sort of cutoff function — or whether it is just a result of a roundabout formulation that will eventually be simplified through new understanding.

The reader can verify this geometrically by considering an enclosing parallelogram and using the formula for the area enclosed between a parabola and a chord. ↩︎
Here I use “curvature” loosely to mean the second and higher order derivatives, and not the strict technical definition of curvature. ↩︎

-1/12 and the area under the sum function

Leave a Reply Cancel reply

Receive new posts by email:

Recent posts:

Categories: