Introduction
First can I say how much I love Onshape. I have no association with the company other than being a user, so you can trust that this is real, genuine puppy love. Onshape provides much of the functionality of parametric CAD systems such as SolidWorks in your browser, which at first sight seems like magic. Since I’m a Linux user and the native CAD landscape on Linux is quite limited, being able to do CAD in a browser works brilliantly for me. Even better, it’s free for non-commercial use.
My first little project in Onshape, several moons ago, was a vertical illuminator for my home-brew microscope. The problem I had was that when using high magnifications — which require the lens very close — I couldn’t get enough light in under the lens to illuminate opaque samples. A vertical illuminator is the solution to this problem, sending light down through the lens via a beamsplitter. I designed the physical parts in Onshape, exported to STL format and uploaded to Hubs (previously 3DHubs); a local maker printed the parts and within a few days I had it back and working.
Scripting in Onshape
Onshape has a scripting language called FeatureScript. FeatureScript allows extending the Onshape interface with domain-specific tools (features as they’re known in Onshape). For example, if you are doing furniture design in Onshape, you can write features that produce panels and joints and then do high-level design in the user interface, rather than having to work with low-level primitives such as lines and boxes. Clearly this can be a huge boon to productivity. Here is a screenshot from one of the Onshape demonstration videos showing a custom box joint feature that, once created, can be used just like built-in features:
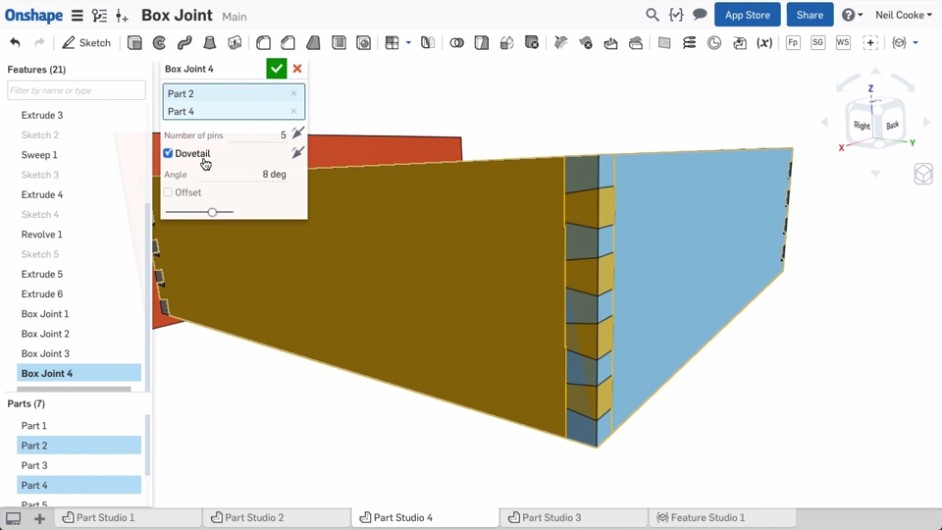
As a programmer and perfectionist I like the idea of writing code to simplify the CAD process rather than spending hours placing parts in a GUI. Prior to Onshape I’ve used OpenSCAD a few times. But for complex designs it gets difficult to mentally keep track of what’s where without having a live preview, and OpenSCAD rendering can get very slow once you start chamfering, filleting and making things pretty. This is where Onshape and FeatureScript shine.
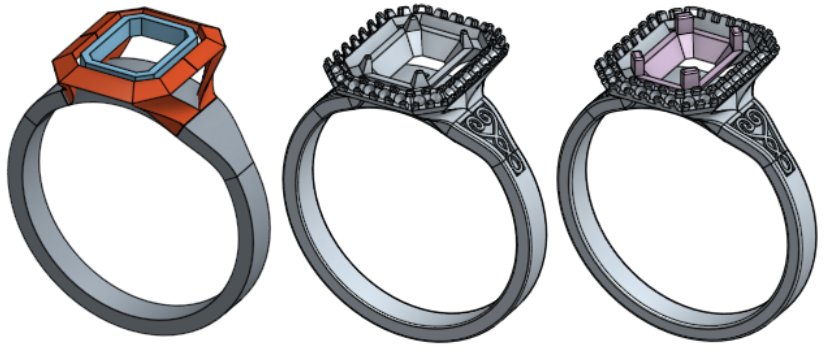
Recently I’ve been doing a bit of jewellery design in Onshape, and this involves a lot of curves and curved surfaces. While I can approximately create the curves I want in the GUI, I wanted to do it programmatically in FeatureScript. Unfortunately a number of the functions that I needed to use were minimally documented so I had to do a lot of trial and error in the process. This article is an attempt to explain some of the missing links for those following in my footsteps.
Onshape is still being developed at a breakneck pace, and since I started writing this article there are now a number of new features related to curves including the option to directly create splines in 3D. I’ll start, though, from the ‘traditional’ way of creating curves in Onshape — by creating them in a 2D sketch and then lofting/extruding/etc. — and I’ll briefly mention 3D curves later in the piece. Continue reading →
BETA![\[ B = \mu_0(H+M) \]](http://zmatt.net/wp-content/ql-cache/quicklatex.com-4af16fb2f9f5749c63024276fe36f01d_l3.png "Rendered by QuickLaTeX.com")
Welcome to the newly redesigned zmatt.net. I seem to only get around to upgrading my personal website once every decade so this is a special day indeed. The biggest change is that I now have a blog here (powered by WordPress). I used to blog on LiveJournal but I was seduced by short attention span media like Facebook, I’m trying to restart the blogging habit.
