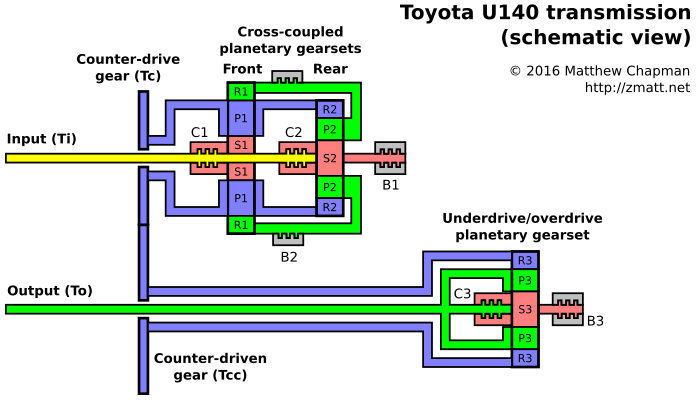
Toyota U140 transmission
Here is a schematic of the U140 automatic transmission used in the RAV4 (not including the torque converter on the front end, or the transfer case and differentials on the rear end):
This is rather daunting at first glance, and I don't recommend trying to understand it before your morning coffee, but after staring at it for a while it does start to make sense.
There are three planetary gearsets, two of which are used to generate the main gear ratios and the third used for overdrive. Each planetary gearset consists of a sun gear (labelled S in the above diagram), a planet carrier and set of planet gears (P), and a ring gear (R). If you have never worked with planetary gears before, it is worth having a look at this video that explains the principles of an automatic transmission, and this page which has some great pictures and information about planetary gears; I found both of these resources very helpful.
In addition to the planetary gearsets, there are three clutches (C1, C2, C3) and three brakes (B1, B2, B3). Engaging C1 connects the input shaft to the front sun gear. Engaging C2 connects the input shaft to the rear sun gear. Engaging B1 stops the rear sun gear (therefore, it is true to assume that B1 and C2 are never engaged at the same time). B2 stops the front ring gear. B3 stops the underdrive sun gear, and C3 gangs it together with the planetary carrier of the same system.
The different gears are then achieved as follows:
- 1st gear: C1, B2, B3
- 2nd gear: C1, B1, B3
- 3rd gear: C1, C2, B3
- 4th gear: C1, C2, C3
- Reverse: C2, B2, B3
How this works is not at all obvious, and I'll work through how the gear ratios are achieved in the following sections. For more detail on how the physical parts fit together, refer to a service manual.
Contents
Calculating the gear ratios
Planetary gear systems seem very complicated until you realise that you can determine the rotation speeds from one simple algebraic equation:
[math] (R+S)T_p = R T_r + S T_s\\ [/math] In this equation, R is the number of teeth on the ring gear, S is the number of teeth on the sun gear, and [math]T_p/T_r/T_s[/math] are the rotation speeds of the planetary carrier, ring and sun respectively. Note that the number of teeth on the planets does not need to be known; it is uniquely determined from [math]P=(R-S)/2[/math]. [1]
Here is the data for the planetary gear systems in the U140 transmission: (source: [2])
| Front planetary gearset | ||
|---|---|---|
| Number of sun gear teeth | S1 | 43 |
| Number of ring gear teeth | R1 | 77 |
| Number of planet gear teeth | P1 | 17 |
| Rear planetary gearset | ||
| Number of sun gear teeth | S2 | 31 |
| Number of ring gear teeth | R2 | 69 |
| Number of planet gear teeth | P2 | 19 |
| Underdrive planetary gearset | ||
| Number of sun gear teeth | S3 | 35 |
| Number of ring gear teeth | R3 | 91 |
| Number of planet gear teeth | P3 | 28 |
The one other piece of information we'll need is the ratio of the counter-drive gears:
| Counter-drive gearset | |
|---|---|
| Number of teeth on counter-driving gear | 52 |
| Number of teeth on counter-driven gear | 53 |
Now let's take a look at how all the gears are obtained from the three planetary gear systems.
3rd and 4th gear
In these high gears, clutches C1 and C2 are both engaged, so the sun gears of the front and rear gear systems are both driven at the input speed ([math]T_i[/math]). Since the planet carrier of the front system is connected to the ring of the rear system, and vice versa, it might be intuitive that the only sensible solution is for everything to rotate at the same speed (if either gearset were to produce a gear ratio greater than 1:1, one would expect the other to also do so by symmetry, but the cross-coupling requires the ratios must be the reciprocal of each other).
Let's work through the equations to prove that's the case:
[math] \begin{cases} (S_1+R_1) T_c = S_1 T_i + R_1 T_x \quad\text{(1)} \\ (S_2+R_2) T_x = S_2 T_i + R_2 T_c \quad\text{(2)} \end{cases} \\ \begin{align} T_x &= \frac{(S_1+R_1) T_c - S_1 T_i}{R_1} &&\text{(from (1))} \\ (S_2+R_2) \left(\frac{(S_1+R_1) T_c - S_1 T_i}{R_1}\right) &= S_2 T_i + R_2 T_c &&\text{(substituting into (2))} \\ (S_2+R_2)(S_1+R_1) T_c - (S_2+R_2) S_1 T_i &= R_1 (S_2 T_i + R_2 T_c) &&\text{(moving $R_1$ over)}\\ (S_2 S_1 + R_2 S_1 + S_2 R_1 + R_2 R_1 - R_2 R_1) T_c &= (S_2 S_1 + R_2 S_1 + S_2 R_1) T_i &&\text{(expanding and grouping)}\\ T_c &= T_i \end{align}\\[/math]
After what seems like an excessive amount of algebra to get to a simple answer, we've proven that the counter-driving gear is spinning at exactly the same rate at the input (1:1); this is called direct drive. This is why clutch C2 is also called the direct drive clutch.
However, the counter-driving gear has 52 teeth while the counter-driven gear has 53 teeth, so there is actually a small reduction in the transfer to the next stage of the transmission.
[math] T_{cc} = \frac{52}{53} T_c\\ [/math]
The only difference between 3rd and 4th gear is in the operation mode of the underdrive/overdrive gear set.
In 4th gear, clutch C3 is engaged and locks the sun gear to the planetary carrier which is connected to the output. A characteristic of planetary gear systems is that if any two components are locked together, the third must have the same speed. We can go through the algebra to prove this, which turns out to be much simpler than last time:
[math]\begin{align} (S_3+R_3)T_o &= S_3 T_o + R_3 T_{cc} \\ R_3 T_o &= R_3 T_{cc} \\ T_o &= T_{cc} \text{ (as expected)} \end{align}\\[/math]
Indeed in fourth gear all three planetary gear systems are in direct drive (1:1), with only the small reduction factor due to the larger number of teeth on the counter-driven gear.
[math]\begin{align} T_o &= \frac{52}{53} T_i \\ &= 0.981 T_i \end{align}\\[/math]
Gear ratios are traditionally given with the output on the denominator, so the gear ratio for 4th gear is quoted in the manual as the reciprocal of this:
| [math]\frac{T_i}{T_o} = 1.019 \text{ (4th gear)}[/math] |
In 3rd gear, brake B3 is engaged and the sun gear is stationary. Then:
[math]\begin{align} (S_3+R_3)T_o &= 0 + R_3 T_{cc} \\ T_o &= \frac{R_3}{R_3+S_3} T_{cc} \\ &= \frac{91}{91+35} T_{cc} \\ &= 0.722 T_{cc} \\ &= 0.709 T_c \\ &= 0.709 T_i \text{ (front two systems in direct drive as before)} \end{align}\\[/math]
| [math]\frac{T_i}{T_o} = 1.411 \text{ (3rd gear)}[/math] |
2nd gear
In 2nd gear, C1 is engaged (connecting the sun of the front system to the input) and B1 is engaged (stopping the sun of the rear system). Then we have:
[math]\begin{cases} (S_1+R_1) T_c &= S_1 T_i + R_1 T_x \\ (S_2+R_2) T_x &= 0 + R_2 T_c \end{cases} \\ \begin{align} T_x &= \frac{R_2}{S_2+R_2} T_c &&\text{(from (2))} \\ (S_1+R_1) T_c &= S_1 T_i + R_1 \frac{R_2}{S_2+R_2} T_c &&\text{(substituting into (1))} \\ \left(S_1 + \left(1-\frac{R2}{S2+R2}\right)R_1\right) T_c &= S_1 T_i &&\text{(grouping)} \\ T_c &= \frac{S_1}{S_1 + \left(1-\frac{R_2}{S_2+R_2}\right)R_1} \\ T_c &= 0.643 T_i \end{align}[/math]
The underdrive system operates in underdrive as for 3rd gear, so:
[math] T_o = 0.709 \times 0.643 T_i\\ [/math]
| [math]\frac{T_i}{T_o} = 2.194 \text{ (2nd gear)}[/math] |
1st gear
In 1st gear, C1 is again engaged (connecting the input to the sun of the front system) but instead of B1 we apply B2 (stopping the ring of the front system). Then:
[math]\begin{align} (S_1 + R_1) T_c &= S_1 T_1 + 0 \\ T_c &= \frac{S_1}{S_1 + R_1} T_i \\ &= 0.358 Ti \end{align}\\[/math]
Again the underdrive system is in the underdrive configuration, so:
[math] T_o = 0.709 \times 0.358 T_i\\ [/math]
| [math]\frac{T_i}{T_o} = 3.938 \text{ (1st gear)}[/math] |
Reverse
In reverse, C2 is engaged (connecting the input to the sun of the rear system) as well as B2 (stopping the planetary carrier of the rear system). Stopping the planetary carrier in a planetary gear system results in a reverse drive. We can once again show this with the algebra:
[math]\begin{align} 0 &= S_2 T_i + R_2 T_c \\ T_c &= -\frac{S_2}{R_2} T_i \\ &= -0.449 T_i \end{align}\\[/math]
As usual the counter-driven gear and underdrive scale this by 0.709:
[math] T_o = 0.709 \times -0.449 T_i\\ [/math]
| [math]\frac{T_i}{T_o} = -3.141 \text{ (Reverse gear)}[/math] |
You can verify against Wikipedia that we've calculated all the gear ratios correctly.
Neutral and park
In neutral and park, no clutches are engaged except for B3. Since neither C1 or C2 are engaged, the input shaft from the engine spins freely, and the wheels drive the rest of the transmission as if it were in third gear. In park, a parking lock pawl is engaged that locks the underdrive planetary carrier to stop it rotating.
(Presumably, B3 is released when the engine stops and the transmission loses oil pressure. However, the underdrive planetary carrier is now held by the parking pawl.)
One-way clutches
There are also two one-way clutches in the U140 transmission that I haven't described above: one operates alongside B2 and the other alongside B3, allowing rotation in one direction but not the other. I believe these are used to smooth out gear changes as follows, although do let me know if I am wrong, I could find very little information about them.
Consider the gear change from 1st to 2nd (or indeed 2nd to 1st). Changing from 1st to 2nd requires releasing brake B2 (the front ring gear) and engaging brake B1 (the rear sun gear). The problem is the timing of this change. If the engagement of B1 comes first, even by milliseconds, the transmission will start jerking to a stop. If the release of B2 comes first, the planetary gear system becomes under-constrained, and the power of the engine starts being transferred into rotating this front ring gear backwards (since it's easy to turn) rather than driving the output (which is harder to turn). The solution is to use a one-way clutch alongside B2. This one-way clutch stops the ring gear rotating backwards when B2 is released, while allowing it to rotate forwards when B1 is then applied.
The gear change from 2nd to 3rd requires changing from B1 to C2. I believe the same problem would occur that, when B1 is released, engine power starts being transferred into slowing down the front ring and driving the rear sun backwards. However, there does not seem to be any special one-way clutch alongside B1 to prevent the rear sun going backwards; perhaps B1-C2 can be done quickly enough that it is not a problem in practice, or there is some other trick used for this change.
The gear change from 3rd to 4th requires changing from B3 to C3. Again, after releasing B3, the underdrive gear system becomes underconstrained, and power will tend to flow into rotating the sun gear backwards rather than into turning the planetary carrier (output) forwards. Here there is indeed a one-way clutch on the underdrive sun gear alongside B3 that will stop this from happening.
U140E vs U140F
There are two variants of the U140: the U140F is used on AWD models and includes a transfer case in the transaxle assembly, while the U140E is used on 2WD vehicles and does not. Otherwise both share the same transmission components described above.